HUB SCIENTISTS EXTEND TRADITIONAL EPIDEMIOLOGIAL MODELS
Most epidemics show infection curves with a typical S-shape. The COVID-19 outbreak, however, shows most infection curves exhibiting a linear growth after the first peak.
Stefan Thurner, Peter Klimek and Rudi Hanel extend traditional epidemiological models by describing the spread of disease as so-called cluster transmission. In this way, they are able to explain the typical linear shape of curves.
A MODEL THAT FINALLY DESCRIBES THE UNTYPICAL SHAPE OF COVID-19 INFECTION CURVES
Hub scientists Stefan Thurner, Peter Klimek and Rudi Hanel are the first to offer an explanation for the linear growth of coronavirus infection curves.
With the first COVID-19 epidemic peak behind them, many countries explained the decrease of infection numbers through non-pharmaceutical interventions. Phrases like “social distancing” and “flatten the curve” have become part of common vocabulary. Yet some explanations still fell short: How could one explain the linear rise of infection curves, which many countries display after the first peak, in contrast to the S-shaped curves expected, from epidemiological models?
In a paper that will be published today in the Proceedings of the National Academy of Sciences of the United States of America (PNAS), CSH scientists are the first ones to offer an explanation for the linear growth of the infection curve.
“At the beginning of the pandemic, COVID-19 infection curves showed the expected exponential growth,” says Stefan. This can be well explained by a so-called snowball effect: An infected person would infect a few others, and in a chain reaction, those would pass the virus on to a few others as well. “With measures like social distancing, governments tried to push the growth rate below the recovery rate and therefore massively reduce the number of new infections. In this logic, however, individuals would have infected less than one other person, and the curve would have flattened, eventually reaching zero—something that, as we know, did not happen,” says Stefan.
“What we saw instead was a constant level of infections with a similar number of new infections every day,” adds co-author Peter Klimek, “To explain this with standard epidemiological models would basically be impossible.” The use of traditional epidemiological models would have required a lot of fine-tuning of parameters, something that would make the model increasingly implausible. “If you want to balance measurements so that the effective reproduction number R stays exactly at 1—something that would explain the linear growth—, you would have to reduce contacts by the same exact and constant percentage. In reality that is extremely unlikely,” Peter adds.
IT IS THE CONTACT NETWORK DENSITY THAT INFLUENCES TRANSMISSION RATES
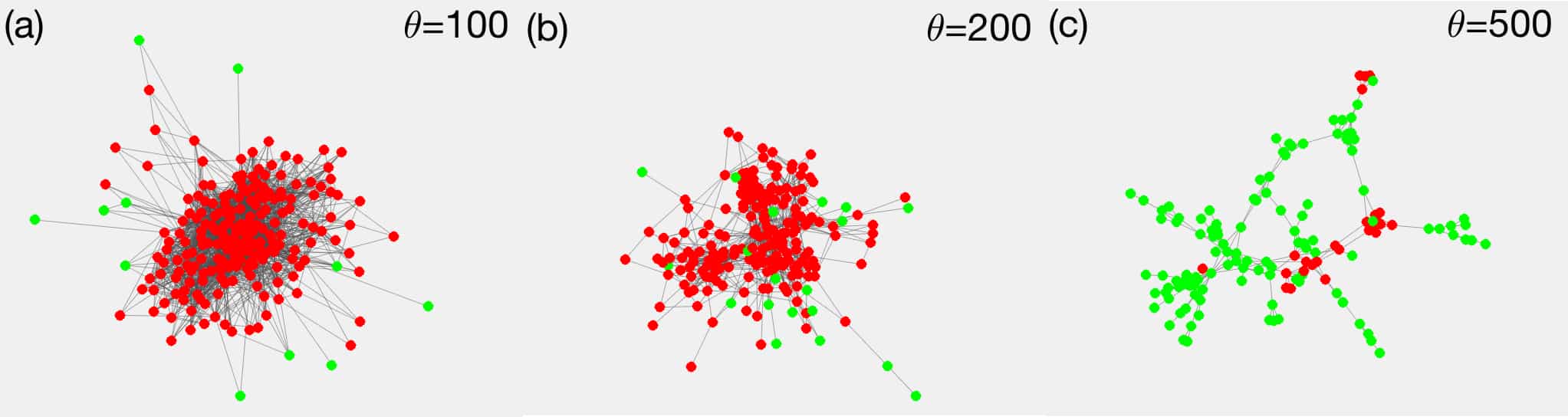
Instead of having to fine-tune parameters, their model allows for a wide range of possibilities that keep the infection curves linear, which explains why linear infection curves appear in so many countries, irrespective of the magnitude of the imposed non-pharmaceutical interventions.
Here are two examples: the U.S. and Austria.
WHAT IF … ?
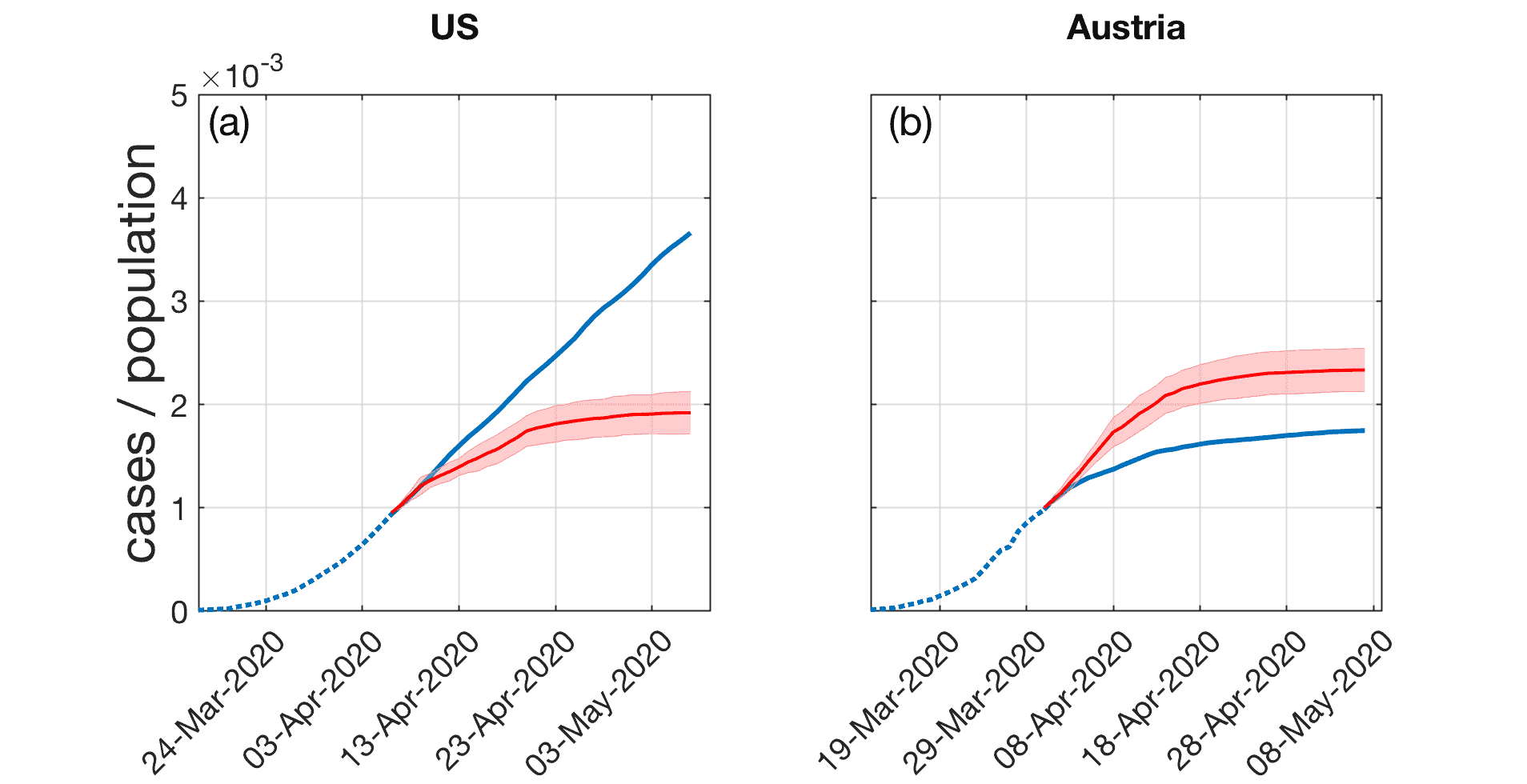
LINEAR CURVES IN THE U.S. AND AUSTRIA
In a further step the scientists compared Austria, a country which responded with a severe lockdown early on, and the United States, which initially did not impose severe measures. According to Peter Klimek, their model works for both scenarios: “Both types of countries showed linear curves, but in the case of the U.S. and other countries like Sweden, these just happened on a much higher level.”
The model not only explains the emergence of a linear growth regime, but also explains why the epidemic may halt below the levels of herd immunity. For the standard modelling procedure, the complexity scientists use a so-called compartmental model with SIR-models, extending it with the described cluster transmission.
But what will happen in the next months, with the potential of numbers rising again? With additional risk factors like people returning from vacation in other countries and more time spent inside, the spread of disease could change. “If infections rise again, there is the potential that linear curves turn to exponential growth again—something people described as a second wave,” Peter concludes.
LIT.:
Stefan Thurner, Peter Klimek, Rudolf Hanel, A network-based explanation of why most COVID-19 infection curves are linear, PNAS August 24, 2020
WARUM SICH COVID-19-INFEKTIONSKURVEN ANDERS VERHALTEN ALS ERWARTET
Mit einem erweiterten Epidemiologie-Modell gelingt es Wissenschaftlern am CSH Vienna, das lineare Wachstum bei Coronavirus-Infektionskurven zu erklären.
Viele Länder erklärten den Rückgang der Infektionszahlen nach dem ersten Höhepunkt der Coronavirus-Pandemie durch „nicht-pharmazeutische Interventionen“ – Ausdrücke wie „social distancing“ und „Abflachen der Kurve“ sind mittlerweile in den Sprachschatz eingegangen. Aber wie ist der lineare Anstieg der Infektionskurven zu erklären, den viele Länder nach dem ersten Peak zeigen, und der in einem Gegensatz zu den S-förmigen Kurven steht, die die gängigen epidemiologischen Modelle erwarten lassen?
In einem Artikel in der aktuellen Ausgabe von PNAS (Proceedings of the National Academy of Sciences of the United States of America) legen Wissenschaftler des Complexity Science Hub Vienna (CSH) und der MedUni Wien erstmal eine Erklärung für diese linearen Infektionsanstiege vor.
„Zu Beginn der Pandemie haben die COVID-19-Infektionskurven das erwartete exponentielle Wachstum gezeigt“, erklärt Stefan Thurner, Präsident des CSH und Professor für die Wissenschaft komplexer Systeme an der Medizinischen Universität Wien. Exponentielles Wachstum lässt sich gut durch den Schneeballeffekt erklären: Eine infizierte Person infiziert ein paar wenige andere, die das Virus ihrerseits an ein paar andere weitergeben – eine Kettenreaktion. „Mit Maßnahmen wie sozialer Distanzierung haben Regierungen versucht, die Wachstumsrate unter die Heilungsrate zu drücken und damit die Zahl der Neuinfektionen massiv zu reduzieren“, so Thurner. „Nach dieser Logik würde jede infizierte Person weniger als eine weitere Person anstecken. Damit würde die Kurve rasch abflachen und schließlich Null erreichen – was bekanntlich aber nicht geschehen ist.“
„Stattdessen sehen wir ein konstantes Infektionsniveau mit einer ähnlichen Anzahl von Neuinfektionen jeden Tag“, ergänzt Koautor Peter Klimek (CSH & Medizinische Universität Wien). „Epidemiologische Standardmodelle können das nicht erklären.“ Um einen solchen linearen Anstieg zu zeigen, müssten die Standardmodelle ständig nachjustiert werden – womit sie aber zunehmend unplausibel werden. “Will man die Messungen so ausgleichen, dass die effektive Reproduktionszahl R genau bei 1 bleibt – was das lineare Wachstum erklären würde –, müsste man die Kontakte um den gleichen exakten und konstanten Prozentsatz reduzieren. In Wirklichkeit ist das äußerst unwahrscheinlich“, so Klimek.
Tatsächlich ist die Wahrscheinlichkeit, in Standardmodellen lineares Wachstum zu sehen, praktisch null, betonen die CSH-Wissenschaftler. „Deshalb haben wir diese Modelle erweitert, indem wir eine andere Form der Ausbreitung annehmen. Wir gehen davon aus, dass sich Krankheitsfälle in kleinen, sehr begrenzten Clustern ausbreiten“, so Thurner. „Die meisten Menschen gehen zur Arbeit, infizieren sich und stecken zwei oder drei Personen zu Hause an. Dann gehen sie wieder zur Arbeit oder zur Schule. Die Infektion breitet sich also eigentlich von Cluster zu Cluster aus.“
Für ihr Verfahren verwenden die Komplexitätswissenschaftler ein so genanntes SIR-Modell, das sie um die beschriebene Clusterübertragung korrigieren.
Die Wissenschaftler zeigen, dass es eine kritische Anzahl von Kontakten gibt – sie bezeichnen sie als „Kontaktnetzwerke-Dichte“ Dc. Liegt die Zahl der Kontakte darunter, kommt es zu linearem Wachstum und einer niedrigen Infektionsrate. Laut den Forschern liegt diese Zahl ungefähr bei 7,2 – wobei sie davon ausgehen, dass die Menschen sich in einem Coronavirus-relevanten Netzwerk von etwa fünf Personen bewegen, durch einen Lockdown sogar nur auf Haushaltsgröße (durchschnittlich 2,5 Personen).
„Wir zeigen also, dass die Veränderung der Infektionskurven von einem S-förmigen zu einem linearen Verhalten eindeutig ein Netzwerkeffekt ist. Diese Dynamik unterscheidet sich grundsätzlich von Superspreader-Ereignissen,“ so Thurner.
Anstatt eine Feinabstimmung der Parameter vornehmen zu müssen, lässt das neue Modell unter unterschiedlichsten Bedingungen lineare Infektionskurven zu, etwa unabhängig vom Ausmaß der getroffenen staatlichen Interventionen. Die Wissenschaftler vergleichen Österreich, ein Land, das schon früh einen strengen Lockdown eingeführt hat, und die Vereinigten Staaten, die zunächst keine strengen Maßnahmen verhängt haben. „Das Modell funktioniert für beide Szenarien“, betont Klimek: „Beide Ländertypen zeigen lineare Kurven. Im Fall der USA – oder auch anderer Länder mit wenig strikten Maßnahmen wie Schweden – passiert das nur auf einem deutlich höheren Niveau.“
Das Modell der Wiener Forscher erklärt nicht nur die Entstehung von linearem Wachstum, sondern auch, dass die Epidemie durch konsequentes Social distancing schon vor Erreichen der Herdenimmunität zum Stillstand kommen könnte.
Aber was wird in den nächsten Monaten passieren, wenn die Zahlen wieder steigen? Mit zusätzlichen Risikofaktoren wie Auslandsurlauben oder mehr Aufenthalten in geschlossenen Räumen könnte sich die Ausbreitung der Krankheit wieder stark ändern. “Wenn die Infektionen stark steigen, kann aus dem linearen Wachstum wieder ein exponentielles werden“, so Klimek. „Dann haben wir die zweite Welle.“